sasauber.blogg.se - Residuals vs the variables minitab express

#RESIDUALS VS THE VARIABLES MINITAB EXPRESS HOW TO#
#RESIDUALS VS THE VARIABLES MINITAB EXPRESS CODE#

#RESIDUALS VS THE VARIABLES MINITAB EXPRESS HOW TO#

Next, we will look at how to fit a simple linear regression. This fitted model can then be subsequently printed, summarized, or visualized moreover, the fitted values and residuals can be extracted, and we can make predictions on new data (values of X) computed using functions such as summary(), residuals(), predict(), etc. A typical call may look likeĪnd it will return a fitted model object, here stored as myfunction. I think the problem might be in coded variables, are uncoded variables converted into coded ones in the same way, or it might be done differently Or the. In R, models are typically fitted by calling a model-fitting function, in our case lm(), with a "formula" object describing the model and a "ame" object containing the variables used in the formula. We will review how to assess these assumptions later in the module.

Normality: For any fixed value of X, Y is normally distributed.

Independence: Observations are independent of each other.

Homoscedasticity: The variance of residual is the same for any value of X.

Stat>DOE>Factorial>Analyze factorial design> Graphs> residuals vs variables. Anyone had same experience Is there anyway i can do this I did try two methods. Minitab does not allow me to slect those text columns. couple of my variables(or factors) are text ( small, large).

Linearity: The relationship between X and the mean of Y is linear. I would to like to draw residuals VS variables graph in minitab.

There are four assumptions associated with a linear regression model: Introduction to Statistical Learning (Springer 2013) Instead of the "line of best fit," there is a " plane of best fit." Here is an example of a linear regression with two predictors and one outcome: The 'simple' part is that we will be using only one explanatory variable. In this course, we will be learning specifically about simple linear regression. The residuals are the fitted values minus the actual observed values of Y. Regression uses one or more explanatory variables ( x) to predict one response variable ( y ). The fitted values (i.e., the predicted values) are defined as those values of Y that are generated if we plug our X values into our fitted model. When we have more than one predictor, we call it multiple linear regression: View Homework Help - from MATH 2209 at Mount Saint Vincent University. The betas are chose such that they minimize this expression:Īn instructive graphic I found on the Internet The betas are selected by choosing the line that minimizing the squared distance between each Y value and the line of best fit. That is, the expected value of Y is a straight-line function of X. When we have one predictor, we call this "simple" linear regression: least squares residuals against the explanatory variable or y if its. Notice that the lines follow a different pattern depending on the deviation from linearity.Regression analysis is commonly used for modeling the relationship between a single dependent variable Y and one or more predictors. In Minitab: Click Stat > Regression > Regression > Fit Regression.

#RESIDUALS VS THE VARIABLES MINITAB EXPRESS CODE#

Here is some example code to see what happens when assumptions are violated x = 1:100 If your regression assumptions are met, you'll get a flat line, as any slice of your residuals should be mean zero (and often normally distributed). If the data is not linear, there will be a pattern to the residuals and this is one way of helping you see that.

In response to your comment asking more about the line:

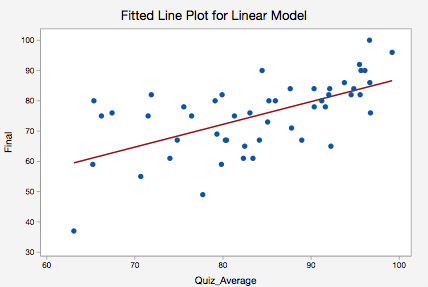
On your plot, this means that the point labeled 25 had a predicted value of about 525 but the residual was around -200, meaning its actual value was closer to 325. Remember that a residual is $e_i = y_i - \hat_i$ which is the true $y_i$ minus what the regression estimates should be the outcome for point $i$. In this case it's pretty flat, which provides evidence that a linear model is reasonable. Give the equation of your regression line. To get a residual plot, select 'Graphs' before clicking 'OK', click in the box 'Residuals versus the variables' and then select your predictor variable. For example, if you fit a linear regression on data that looked like $y = x^2$ you'd see a noticeable bowed shape. Minitab Express does provide a scatterplot automatically with the regression output. Basically, it's smoothing over the points to look for certain kinds of patterns in the residuals. Again we will use a transformation of variables and refer to Section 7.3, to express the. The red line is a LOWESS fit to your residuals vs fitted plot. Includes a Data Disk Designed to Be Used as a Minitab File.